CONVERSION DE OCTAL A BINARIO

Conversión de Octal convertir (16 a Binario o Base 2
Vamos a ver las instrucciones para pasar el número convertir que está en formato Octal a Binario natural
La conversión entre Octal y Binario es casi inmediata,
ya que cada digito Octal tiene una correspondecia directa con un conjunto de
3 digitos en binario, por ser ambos bases multiplos de 2.
Asi el número Octal convertir(16 estará formado
por 9 grupos de 3 números binarios.
Esta misma situacion ocurre con la conversion hexadecimal a binario pero con grupos de 4.
Para realizar la conversion tomo cada uno de los digitos Octal
y los paso a grupos de 3 digitos binarios con la siguiente tabla
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 000 | 001 | 010 | 011 | 100 | 101 | 110 | 111 |
Para el numero convertir (8 hacemos los siguientes calculos
El valor c(16 en binario es c(2
El valor o(16 en binario es o(2
El valor n(16 en binario es n(2
El valor v(16 en binario es v(2
El valor e(16 en binario es e(2
El valor r(16 en binario es r(2
El valor t(16 en binario es t(2
El valor i(16 en binario es i(2
El valor r(16 en binario es r(2
Para finalizar lo pongo todo junto
y queda que convertir (8
equivale a c o n v e r t i r(2 y
sin los guiones es convertir(2
|
Tutorial Convertir Octal a Binario
En este tutorial vamos a aprender todo sobre Convertir Octal a Binario
El sistema octal es un sistema de numeración que es muy parecido al decimal pero solo tiene 8 símbolos ya que su base es 8 osea que solo cuenta con los números del {0,1,2,3,4,5,6,7}
Los sistemas de numeración que tienen su base múltiplo de dos son muy fácil transformarlos al binario como el sistema Octal cuya base es 8 y cuya traducción al binario es inmediata.
Para pasar del octal al binario debemos transformar cada cifra independientemente al binario usando la transformación binario-decimal o la siguiente tabla
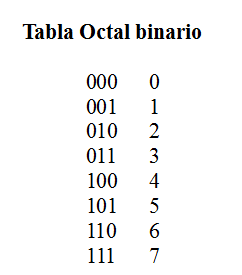
Tabla Octal binario
000 (2 = 0(8
001(2 = 1 (8
010(2 = 2 (8
011(2 = 3 (8
100(2 = 4 (8
101(2 = 5 (8
110(2 = 6 (8
111(2 = 7(8
Por ejemplo el 237 sería 2= 010 3 = 011 7=111 luego seria 010011111
|
CONVERSION DE BINARIO A OCTAL
En este tutorial vamos a aprender todo sobre Conversor Binario Octal
El sistema octal es un sistema de numeración que es muy parecido al decimal pero solo tiene 8 símbolos ya que su base es 8 osea que solo cuenta con los números del {0,1,2,3,4,5,6,7}
Los sistemas de numeración que tienen su base múltiplo de dos son muy fácil transformarlos al binario como el sistema Octal cuya base es 8 y cuya traducción al binario es inmediata.
Para pasar del octal al binario debemos transformar cada cifra independientemente al binario usando la transformación binario-decimal o la siguiente tabla
Tabla Octal binario
000 (2 = 0(8
001(2 = 1 (8
010(2 = 2 (8
011(2 = 3 (8
100(2 = 4 (8
101(2 = 5 (8
110(2 = 6 (8
111(2 = 7(8
Por ejemplo el 237 sería 2= 010 3 = 011 7=111 luego seria 010011111
Ejemplo Binario Octal
Para convertir binario a octal solo debemos hacer grupos de 3 los dígitos binarios desde la derecha y convertirlos igualmente con la tabla o con la conversión binario decimal, con la idea de que si faltan 0 se le añaden por la izquierda
1110101011010101010 =
Agrupo de 3 en 3 y añado dos ceros al ultimo
001 110 101 011 010 101 010 =
Convierto según la tabla
001 = 1
110 = 6
101 = 5
011 = 3
010 = 2
101 = 5
010 = 2
el numero octal es 1653252